Closure Temperature

I've alluded in some of my previous posts (aquí und hier) to one of the fundamental concepts of thermochronology, the idea of a closure temperature. Today I ended up re-reading some of the first thermochronology papers I ever read, back in the day. Long story short I was thinking about what the term closure temperature means today, and decided that after a year of blogging it was high time the the world's foremost thermochronology blog did something with this fundamental idea.

Most people trace the idea of a closure temperature, or at least the term, to a classic 1973 paper written by Martin Dodson (Dodson, 1973). The issue, as Dodson describes, is that some radioactive daughter products (he was concerned with Sr and Ar, but this also applies to other daughter products) are mobile long after a rock has crystallized. By mobile, I mean that they can readily move out of a crystal. If the daughter products are lost, there is no way to calculate a radiometric age. Well, I take that back, you would calculate an age of zero. Once a mineral cools enough, then the daughter product can accumulate, and the radiometric "clock" has started. Before I go on, I will make another self reference to a post where I point out that OG, Original Geochronologist R.J. Strutt mentioned this problem a century ago. OK, that's done.

It would be nice if this transitional temperature were finite. That is, that there was a set and known temperature above which the daughter product diffused readily, and below which the daughter product is entirely retained. This theoretical temperature is called the closure temperature (usually written as T_c); the temperature below which the mineral is closed to diffusion (in the past few years I've noticed this called a Dodsonian closure temperature, in part recognizing Dodson's contribution but also recognizing the necessary simplifying assumptions his 1973 paper made, more on that in the next paragraph.) In the real world, however, there is actually a broad range of temperatures over which daughter products can, and do, diffuse. This range of temperatures is often referred to as a partial retention zone.

When you start trying to pin down exactly what that means, physically, it gets tricky. The truth is, things like Ar and He never really stop diffusing out of crystals. Even at room temperature, for example, Ar and He diffuse, just so slowly that it really doesn't make much of a difference. Dodson of course realized this, and provides a very zen definition of what he thinks the term closure temperature means:

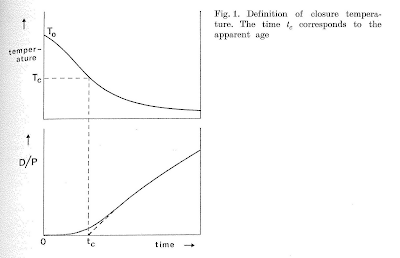
Closure temperature of a geochronological system may be defined as its temperature at the time corresponding to its apparent age.

So you see, grasshopper, it is what it was. This of course gives no direct way to assign a temperature to an age. Dodson showed the idea graphically this way:

The top graph shows the thermal history of a sample, in the form of temperature decreasing with time. The bottom graph shows the daughter to parent ratio of the sample over the same time interval, with the assumption that at high temperatures the daughter escapes easily, so the ratio is zero. At some temperature, daughters start to be retained, and as cooling continues, the daughter/parent ratio increases with time. If you use the present day ratio to calculate an age, and then see what temperature the rock was at at that time, well, that is the closure temperature of your system. Unfortunately, as I'll talk about in a bit, rocks don't come with the top graph, or even the bottom one for that matter, all we have is the present day daughter to parent ratio.

Mathematically, Dodson worked out a way to calculate the closure temperature, given a few assumptions and with a few other knowns thrown in. Here is the Dodsonian closure temperature equation

The best description I've ever heard of a closure temperature was when I was in grad school, a visiting über-thermochronologist said that a closure temperature is really just thermodynamic shorthand for a whole suite of physical and chemical properties. In the equation above, R is the gas constant, E_a is the activation energy of the daughter product's diffusion in the mineral of interest, A is a geometric factor considering the shape of the host mineral the daughter is diffusing out of, D_o is the frequency factor (another diffusive constant describing the rate the daughter product), a is the size of the diffusion domain in the mineral of interest, and dT/dt is the cooling rate. D_o and E_a are things that are determined through laboratory diffusion experiments, A and a are specified depending on the situation. I'd like to point out a few things about the equation. First, of all the inputs, E_a is the strongest control on the closure temperature; the other variables are locked up in a natural log term. Second, you have to input a cooling rate. But how do you know the cooling rate without thermochronologic ages and closure temperatures? Laboratory measurements of of the diffusive parameters are actually pretty good, but assigning a closure temperature to a system (say He in apatite, or Ar in biotite) still requires knowing a priori the cooling rate. In practice, people often quote a closure temperature assuming an average cooling rate, which is almost as meaningless as saying average geothermal gradient, and which should read geologically reasonable cooling rate (just like it should be a geologically reasonable geothermal gradient,) but I digress. In truth, for a wide range of geologically reasonable cooling rates, the range of closure temperatures isn't that great, certainly within an acceptable range of uncertainties for most applications. Where you run into problems are on the extreme slow cooling end of the spectrum. Minerals that cool very slowly can have drastically reduced closure temperatures (some slowly cooled Chinese samples I worked on have apatite He closure temperatures of about 57°C, about 30% lower that the quoted closure temperature of He in apatite.) The situation gets even more tricky, because this definition of a closure temperature, at least the derivation of the equation, assumes cooling that is linear in 1/T (or that in a time versus inverse temperature plot the thermal history is linear.) Dodson explains why he did this in the paper, and why it is a reasonable assumption for the purpose of the paper, but you can probably guess that rocks that have experienced very complex thermal histories that include perhaps prolonged time at moderate temperatures and/or cycles of heating and cooling will not fit this model.

The upshot of all of this, in my opinion, is that by themselves, thermochronologic ages are meaningless. They are non-unique, and therefore just numbers. Assigning meaning to a thermochronologic age requires external constraints, namely a good understanding of the geology of your study area (good maps, cross sections, and tectonic reconstructions) and multiple thermochronologic controls. There are some excellent software packages that allow you to use many different thermochronometers at once to iteratively constrain each other, usually considering many potential variables are deciding what thermal histories are consistent with all of the available data. My personal favorite is Rich Ketcham's HeFTy. But it all really starts with the geology.

Like many complications in science, the problems inherent in assigning a temperature to a thermochronologic age are increasingly being turned into tools savvy thermochronologists can actually use to their advantage. As I've said before, calculating a geochronologic or thermochronologic age is simple and straightforward. Assigning geologic meaning to that age takes time. It turns out that this problem is especially important to the understanding of the "low temperature" thermochronometers. Since these have seen a huge boom in use and importance in the past decade, it is no wonder that the problem of what closure means is
receiving more and more attention.

I hesitated at including this as the final figure, but decided to include it with a few disclaimers. First, these are all approximate range of closure temperatures for common thermochronologic systems assuming cooling rates of ~10-100 °C/My, and, I do not mean to imply that U-Pb zircon has a classic closure temperature, only that Pb is retained in zircon at exceptionally high temepratures, and typically is more reflective of the time of crystallization than of cooling through a specific temperature. Also, deciding what thermal importance to assign to your particular thermochronologic age requires a great deal of thinking, that is, these temperatures are relevant for the kinds of systems and tectonic settings I typically study, not necessarily those you happen to study. For example, if you work in hydrothermally altered areas, all bets are off. That being said.

References, etc..

Dodson, M.H., 1973, Closure Temperature in Cooling Geochronological and Petrological Systems, Contributions to Mineralogy and Petrology, v. 40, pp. 259-274.

And, although it is focused on the ⁴⁰Ar/³⁹Ar world, Ian McDougall and T. Mark Harrison's excellent book Geochronology and Thermochronology by the ⁴⁰Ar/³⁹Ar Method (Oxford University Press, 1999) gives an excellent discussion of closure temperatures, their meaning, and their derivation.